Dlaczego Platon i Kepler są potrzebni dzieciom?

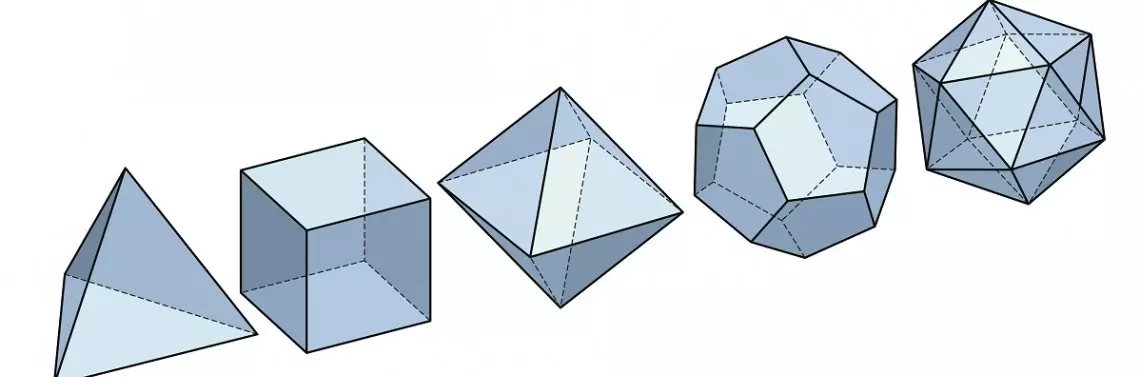
Dla każdej osoby, która w swym życiu spotkała się z konkretnymi modelami origami, matematyczny aspekt tej sztuki rodzi się jako pierwsza myśl. Płaszczyzna origami to kwadratowa kartka papieru, którą w początkowych fazach tworzenia formy składa się, przede wszystkim wykorzystując jej geometrię. Dla wielu matematyków fascynujący świat modułowych (wieloelementowych) form przestrzennych, w których jeden element jest zbudowany tak jak pozostałe, a wszystkie łączą się bez użycia kleju, to konstrukcyjny raj i odkrywanie nie tylko tradycyjnych brył platońskich – sześcianu czy czworościanu foremnego itd. To także możliwość tworzenia ich pochodnych, swoistych transformacji w procesach powstawania bardziej skomplikowanych wielościanów, których imponujące nazwy, np. sześcio- czy ośmiościan rombowy, budzą przerażenie u tych, którzy wmówili sobie, iż nie posiadają wyobraźni przestrzennej. Właśnie ta matematyczna podstawa sztuki origami (choć niejedyna) przyciąga do niej tych jej pasjonatów, którzy poprzez zabawę w składanie papieru rozwijają swoje matematyczne pasje. Opracowują wzory matematyczne opisujące liczbę wierzchołków, ścian czy krawędzi w stworzonym przez siebie wielościanie, przewidują możliwość powstania takiej czy innej liczby wierzchołków jednorodnych podczas składania pojedynczej formy origami itd.

Interdyscyplinarny wymiar sztuki składania papieru

Przedstawiony krótko przeze mnie matematyczny wymiar origami nie jest kompletny, ponieważ drugą podstawą sztuki origami jest kinetyka, czyli nauka o zachowaniu ciał w ruchu. To właśnie dzięki kinetyce bardzo poszerza się pole matematycznych doświadczeń człowieka, który bawi się, składając papier. Nie tylko ruch dłoni, ale też optymalny ruch całego organizmu podczas modelowania papierowych form an...